2.5 More examples 2

Let’s keep going with exmaples using flights data.

Previously, we find that the congestion at the airports is unlikely the cause of delays. Then, what else may explain the patterns of delays? Recall that earlier we observe that some airlines have longer delays than others for NYC-MSP flights. Are some airlines responsible for the delays? Let’s take a look at the average delays by carrier.

stat_carrier <- flights %>% 
  group_by(carrier) %>%
  summarise(n_obs = n(),
            dep_delay = mean(dep_delay, na.rm = TRUE),
            arr_delay = mean(arr_delay, na.rm = TRUE)
            ) %>% 
  left_join(airlines, by="carrier") %>%
  arrange(desc(n_obs)) 

stat_carrier %>% kable(digit=2)

carrier	n_obs	dep_delay	arr_delay	name
UA	58665	12.11	3.56	United Air Lines Inc.
B6	54635	13.02	9.46	JetBlue Airways
EV	54173	19.96	15.80	ExpressJet Airlines Inc.
DL	48110	9.26	1.64	Delta Air Lines Inc.
AA	32729	8.59	0.36	American Airlines Inc.
MQ	26397	10.55	10.77	Envoy Air
US	20536	3.78	2.13	US Airways Inc.
9E	18460	16.73	7.38	Endeavor Air Inc.
WN	12275	17.71	9.65	Southwest Airlines Co.
VX	5162	12.87	1.76	Virgin America
FL	3260	18.73	20.12	AirTran Airways Corporation
AS	714	5.80	-9.93	Alaska Airlines Inc.
F9	685	20.22	21.92	Frontier Airlines Inc.
YV	601	19.00	15.56	Mesa Airlines Inc.
HA	342	4.90	-6.92	Hawaiian Airlines Inc.
OO	32	12.59	11.93	SkyWest Airlines Inc.

While we see some differences, the simple average of delays over various routes, days, and hours of flights may not be a good measure for the comparison across carriers. For example, some carriers may serve the routes and hours that tend to have more delays. Also, given that our dataset covers only the flights from New York City, the comparison may not be nationally representative since carriers use different airports around the country as their regional hubs.

For our purposes, instead of delays, let’s compare the average air time among carriers, for whihch we can account for flight’s destination and timing. The differences in air time may indicate some efficiency differences.

Let’s first check how air time relates to flight distance.

flights %>% 
  filter (month == 1, day == 1, !is.na(air_time)) %>%
  ggplot(aes(x = distance, y = air_time)) + 
  geom_point(alpha = 0.05)  +  
  geom_smooth()

## `geom_smooth()` using method = 'loess'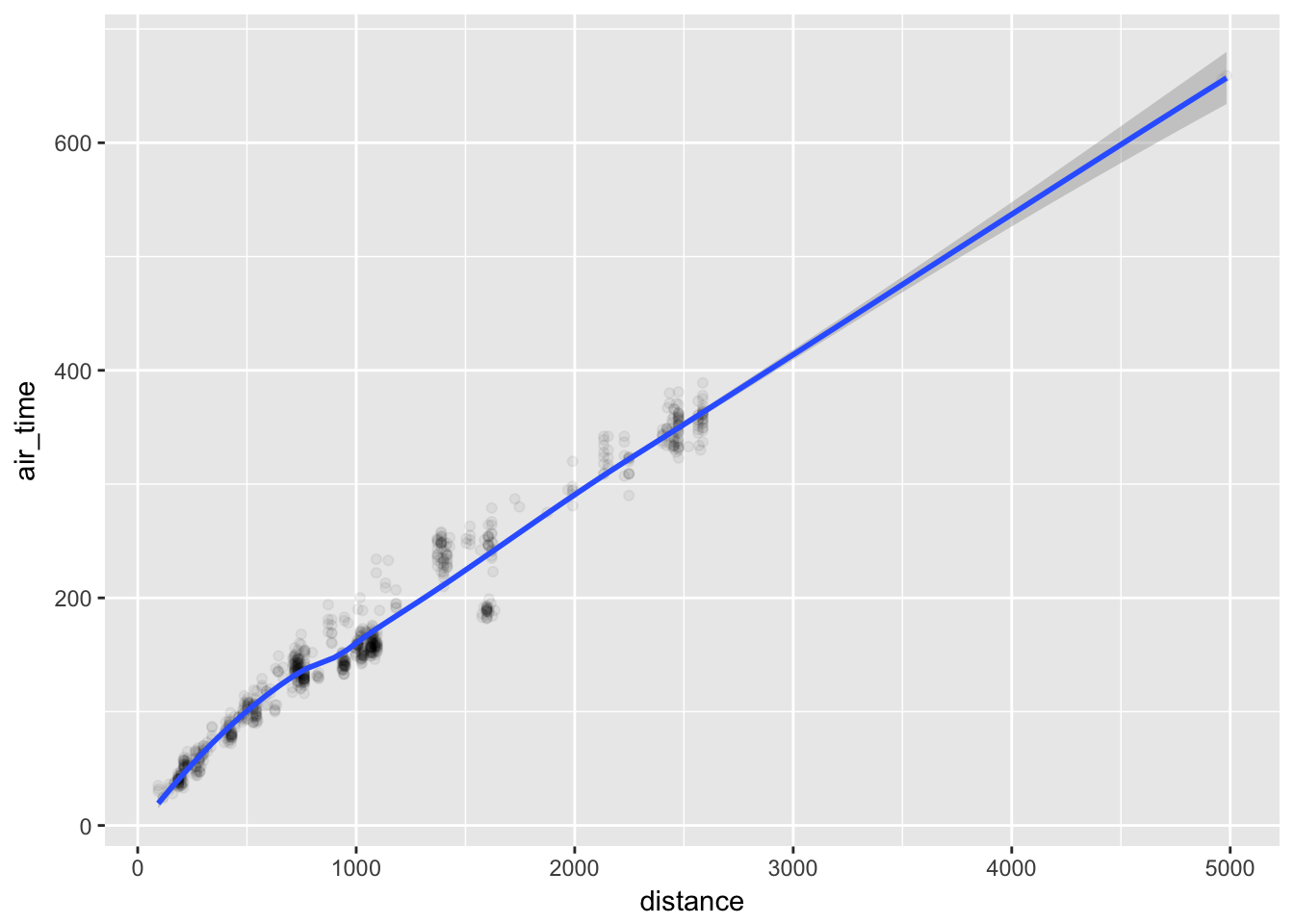

air_time and distance show a general linear relationship. We can better account for this relationship if we calculate the average air time for each flight destination from New York City.

First, consider using a simple linear regression model of air time to account for varying destinations. The idea is to estimate the regression-mean air time for each destination, remove the destination effects from the total variation of air time, and then compare that across carriers.

# make a copy of flights data
flights2 <- flights

flights2 <- flights2 %>%  # handle missing data as NA 
  mutate( idx_na1 = is.na(air_time) | is.na(dest) )

res <- flights2 %>%  # estimate a linear model and obtain residuals 
  with( 
   lm( air_time ~ 0 + as.factor(dest), subset=!idx_na1)  
        # lm() estimates a linear model. 
        # "y ~ x"" is the formula for regressing y on x. 
        # "y ~ 0 + x" removes the intercept from the model. 
        # as.factor() converts "dest" to a factor (categorical) class
        # which is used as a set of dummy variables in the regression.  
   ) %>% 
  residuals()

summary(res)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
## -57.574  -6.909  -0.953   0.000   5.862 144.317

# define a variable containing a vector of NA
# replace rows with idx_na1 == FALSE
flights2$res <- NA
flights2$res[!flights2$idx_na1] <- res 

flights2 %>% 
  group_by(carrier) %>%
  summarise(
    mean_res = mean(res, na.rm = TRUE), # mean residual by carrier 
    sd_res = sd(res, na.rm = TRUE)
    ) %>%
  left_join(stat_carrier, by="carrier") %>% 
  select(carrier, name, n_obs, dep_delay, arr_delay, mean_res, sd_res) %>% 
  arrange(-n_obs) %>% 
  kable(digit=2)

carrier	name	n_obs	dep_delay	arr_delay	mean_res	sd_res
UA	United Air Lines Inc.	58665	12.11	3.56	-0.87	14.59
B6	JetBlue Airways	54635	13.02	9.46	0.28	11.55
EV	ExpressJet Airlines Inc.	54173	19.96	15.80	-0.37	8.94
DL	Delta Air Lines Inc.	48110	9.26	1.64	-0.20	12.32
AA	American Airlines Inc.	32729	8.59	0.36	0.68	13.86
MQ	Envoy Air	26397	10.55	10.77	0.45	8.87
US	US Airways Inc.	20536	3.78	2.13	-0.42	9.43
9E	Endeavor Air Inc.	18460	16.73	7.38	0.84	8.76
WN	Southwest Airlines Co.	12275	17.71	9.65	0.16	12.55
VX	Virgin America	5162	12.87	1.76	3.26	17.58
FL	AirTran Airways Corporation	3260	18.73	20.12	1.16	8.75
AS	Alaska Airlines Inc.	714	5.80	-9.93	-2.13	16.17
F9	Frontier Airlines Inc.	685	20.22	21.92	3.12	15.16
YV	Mesa Airlines Inc.	601	19.00	15.56	-0.05	7.06
HA	Hawaiian Airlines Inc.	342	4.90	-6.92	5.64	20.69
OO	SkyWest Airlines Inc.	32	12.59	11.93	1.02	7.26

It appears to make sense that the average air time is longer for low-cost carriers such as Virgin America, Frontier Airlines, and Hawaiian Airlines. The differences across other carriers, on the other hand, appear small relative to standard errors. To get a sense of whether these differences have any statistical significance, let’s use t-test to compare the mean residual between United Airlines and American Airlines.

# t-test comparing UA vs AA for the mean air time 
flights2 %>%
  with({
    idx_UA <- carrier == "UA"
    idx_AA <- carrier == "AA"
    t.test(res[idx_UA], res[idx_AA])
    })

## 
##  Welch Two Sample t-test
## 
## data:  res[idx_UA] and res[idx_AA]
## t = -15.722, df = 68826, p-value < 2.2e-16
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -1.741133 -1.355142
## sample estimates:
##  mean of x  mean of y 
## -0.8689523  0.6791852

With a large number of observations, a seemingly small difference in the means often turns out to be statistically significant. Nonetheless, the average difference of about 1.5 minute air time per flight appears very small.

In fact, we can do this sort of pair-wise comparison all at once using a regression. Using carrier fixed effects in addition to destination fixed effects, we can directly compare the mean effects across carriers. We will set United Airlines to be a reference of the carrier fixed effects, so that the fixed effect for United Airlines is set to zero (i.e., omitted category), from which the fixed effects of all other airlines are estimated.

flights2$carrier <- relevel(factor(flights2$carrier), ref="UA")  
# reference level is United Airlines
flights2$carrier %>% table()

## .
##    UA    9E    AA    AS    B6    DL    EV    F9    FL    HA    MQ    OO 
## 58665 18460 32729   714 54635 48110 54173   685  3260   342 26397    32 
##    US    VX    WN    YV 
## 20536  5162 12275   601

flights2 %>% 
  with({
    n_carrier <- unique(carrier) %>% length()
    n_dest <- unique(dest) %>% length() 
    print(paste('There are', n_carrier, 'distinct carriers and', 
                n_dest,'distinct destinations in the data.' ))
  })

## [1] "There are 16 distinct carriers and 105 distinct destinations in the data."

With 16 carriers and 105 destinations minus 2 reference levels for carriers and destinations, the total of 119 coefficients will be estimated for the fixed effects.

f1 <- flights2 %>%
 with(
   lm( air_time  ~  as.factor(carrier) + as.factor(dest) )  
    # fixed effects for carriers and destinations
 )

tidy(f1)[1:20,] # show the first 20 coefficients

##                    term     estimate  std.error    statistic       p.value
## 1           (Intercept)  247.9884874 0.75069658  330.3445016  0.000000e+00
## 2  as.factor(carrier)9E    1.8015498 0.12723996   14.1586788  1.702649e-45
## 3  as.factor(carrier)AA    1.9326712 0.09731105   19.8607572  1.002388e-87
## 4  as.factor(carrier)AS   -1.9071536 0.49596319   -3.8453531  1.204017e-04
## 5  as.factor(carrier)B6    1.1808039 0.08495098   13.8998267  6.535025e-44
## 6  as.factor(carrier)DL    0.7531812 0.08722600    8.6348244  5.907432e-18
## 7  as.factor(carrier)EV    0.4174574 0.11044837    3.7796605  1.570702e-04
## 8  as.factor(carrier)F9    3.8891981 0.48090201    8.0872985  6.120836e-16
## 9  as.factor(carrier)FL    2.6434074 0.27600661    9.5773336  1.002386e-21
## 10 as.factor(carrier)HA   11.0125104 0.89821710   12.2604106  1.503557e-34
## 11 as.factor(carrier)MQ    1.4592669 0.11892133   12.2708590  1.321669e-34
## 12 as.factor(carrier)OO    1.8091432 2.21222472    0.8177936  4.134757e-01
## 13 as.factor(carrier)US    0.1319337 0.13826299    0.9542230  3.399715e-01
## 14 as.factor(carrier)VX    4.5298528 0.18441295   24.5636378 4.086448e-133
## 15 as.factor(carrier)WN    1.2226161 0.17520980    6.9780125  2.999500e-12
## 16 as.factor(carrier)YV    0.5167461 0.52737831    0.9798395  3.271661e-01
## 17   as.factor(dest)ACK -207.1011095 1.04478912 -198.2228803  0.000000e+00
## 18   as.factor(dest)ALB -216.6188634 0.95130943 -227.7059972  0.000000e+00
## 19   as.factor(dest)ANC  165.1365126 4.26930687   38.6799351  0.000000e+00
## 20   as.factor(dest)ATL -136.1282095 0.75641976 -179.9638460  0.000000e+00

# a function to clean up the coefficient table above  
clean_lm_rlt <- function(f) {
  # keep only rows for which column "term" contains "carrier"  e.g., rows 2 to 16 above
  rlt <- tidy(f) %>% filter(grepl("carrier",term)) 

  # create column named carrier 
  rlt <- rlt %>% mutate(carrier = gsub('as.factor\\(carrier\\)','', term)) 

  # drop column term
  rlt <- rlt %>% select(-term)
  
  # add columns of carrier, name, and n_obs from the stat_carrier data frame
  stat_carrier %>%  
    select(carrier, name, n_obs) %>%
    left_join(rlt, by="carrier") 
}

clean_lm_rlt(f1) %>% kable(digit=2)

carrier	name	n_obs	estimate	std.error	statistic	p.value
UA	United Air Lines Inc.	58665	NA	NA	NA	NA
B6	JetBlue Airways	54635	1.18	0.08	13.90	0.00
EV	ExpressJet Airlines Inc.	54173	0.42	0.11	3.78	0.00
DL	Delta Air Lines Inc.	48110	0.75	0.09	8.63	0.00
AA	American Airlines Inc.	32729	1.93	0.10	19.86	0.00
MQ	Envoy Air	26397	1.46	0.12	12.27	0.00
US	US Airways Inc.	20536	0.13	0.14	0.95	0.34
9E	Endeavor Air Inc.	18460	1.80	0.13	14.16	0.00
WN	Southwest Airlines Co.	12275	1.22	0.18	6.98	0.00
VX	Virgin America	5162	4.53	0.18	24.56	0.00
FL	AirTran Airways Corporation	3260	2.64	0.28	9.58	0.00
AS	Alaska Airlines Inc.	714	-1.91	0.50	-3.85	0.00
F9	Frontier Airlines Inc.	685	3.89	0.48	8.09	0.00
YV	Mesa Airlines Inc.	601	0.52	0.53	0.98	0.33
HA	Hawaiian Airlines Inc.	342	11.01	0.90	12.26	0.00
OO	SkyWest Airlines Inc.	32	1.81	2.21	0.82	0.41

The “estimate” column shows the mean difference in air time comapred to United Airlines, accounting for the flight destination. The estimate tends to be more precise (i.e., smaller standard errors) for carriers with a larger number of observations. This time, we find that Virgin America, Air Tran, Frontier Airlines, and Hawaiian Airlines tend to show particularly longer air times than United Airlines.

Next, let’s take a step further to account for flight timing as well. We can do this by adding fixed effects for flight dates and hours.

flights2 <- flights2 %>%
  mutate( date_id = month*100 + day )

flights2$date_id %>% unique() %>% length()

## [1] 365

f2 <- flights2 %>%
 with(
   lm( air_time ~  as.factor(carrier) + as.factor(dest) +
        + as.factor(date_id) + as.factor(hour) )
 )

lm_rlt2 <- clean_lm_rlt(f2)
lm_rlt2 %>% kable(digit=2)

carrier	name	n_obs	estimate	std.error	statistic	p.value
UA	United Air Lines Inc.	58665	NA	NA	NA	NA
B6	JetBlue Airways	54635	1.60	0.07	22.50	0.00
EV	ExpressJet Airlines Inc.	54173	0.61	0.09	6.67	0.00
DL	Delta Air Lines Inc.	48110	0.95	0.07	13.03	0.00
AA	American Airlines Inc.	32729	1.84	0.08	22.81	0.00
MQ	Envoy Air	26397	1.45	0.10	14.70	0.00
US	US Airways Inc.	20536	0.17	0.11	1.51	0.13
9E	Endeavor Air Inc.	18460	1.57	0.11	14.72	0.00
WN	Southwest Airlines Co.	12275	1.14	0.15	7.82	0.00
VX	Virgin America	5162	4.85	0.15	31.57	0.00
FL	AirTran Airways Corporation	3260	2.19	0.23	9.58	0.00
AS	Alaska Airlines Inc.	714	-2.55	0.41	-6.21	0.00
F9	Frontier Airlines Inc.	685	3.31	0.40	8.29	0.00
YV	Mesa Airlines Inc.	601	0.32	0.44	0.73	0.46
HA	Hawaiian Airlines Inc.	342	11.79	0.75	15.80	0.00
OO	SkyWest Airlines Inc.	32	7.63	1.83	4.17	0.00

lm_rlt2 %>% filter(carrier!='UA') %>%
  ggplot(aes(x = carrier, y = estimate)) + geom_col() +
  labs(title = "Mean Air Time Compared to United Airlines")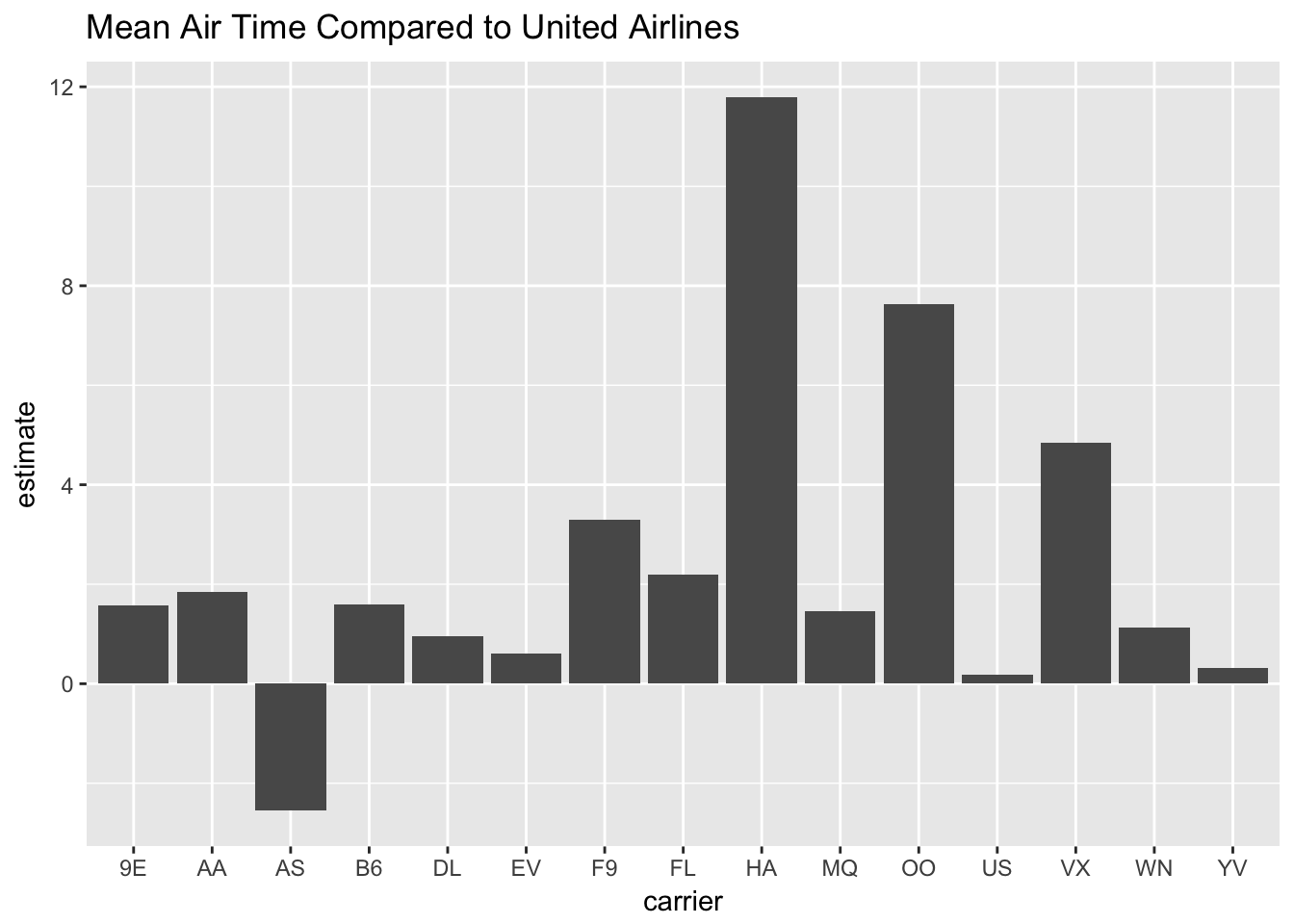

The results are similar to the previous linear mode except that this time SkyWest Airlines shows much longer air time.

Our final model is a check for the robustness of the above results. Let’s replace the date and hour fixed effects in the previous model with date-hour fixed effects (i.e., the interaction between date and hour). We could add such fixed effects using time_hour variable defined above. However, that would mean adding nearly 7,000 dummy variables to our linear regression, which is computationally intensive.

To work around this issue, we approximate this estimation by pre-processing the dependent variable. Specifically, we calculate the average air time for each combination of time_hour and dest and define a new dependent variable by subtracting this average value from the original air time variable (i.e., the new variable is centered at zero-mean for each combination of time_hour and dest). Then, we estimate a linear model with carrier and destination fixed effects.

## Adding time_hour fixed effects is computationally intensive 
# f1 <- flights %>%
#  with(
#    lm( air_time  ~  as.factor(carrier) + as.factor(dest) + as.factor(time_hour))   
#  )

unique(flights2$time_hour) %>% length()  # 6,936 unique time_hour 

## [1] 6936

flights2 <- flights2 %>% 
  group_by(dest, time_hour) %>%   
  mutate(
    air_time_centered = air_time - mean(air_time, na.rm=TRUE) 
  )

f3 <- flights2 %>%
 with(
   lm( air_time_centered  ~  as.factor(carrier) + as.factor(dest) )
 )
  
lm_rlt3 <- clean_lm_rlt(f3)
lm_rlt3 %>% kable(digit=2) # Note: standard errors, t-stat, and p-val are incorrect

carrier	name	n_obs	estimate	std.error	statistic	p.value
UA	United Air Lines Inc.	58665	NA	NA	NA	NA
B6	JetBlue Airways	54635	0.82	0.03	32.24	0.00
EV	ExpressJet Airlines Inc.	54173	0.88	0.03	26.50	0.00
DL	Delta Air Lines Inc.	48110	0.52	0.03	19.85	0.00
AA	American Airlines Inc.	32729	1.20	0.03	41.06	0.00
MQ	Envoy Air	26397	1.00	0.04	27.84	0.00
US	US Airways Inc.	20536	-0.09	0.04	-2.21	0.03
9E	Endeavor Air Inc.	18460	1.27	0.04	33.07	0.00
WN	Southwest Airlines Co.	12275	1.30	0.05	24.70	0.00
VX	Virgin America	5162	3.47	0.06	62.59	0.00
FL	AirTran Airways Corporation	3260	1.78	0.08	21.48	0.00
AS	Alaska Airlines Inc.	714	-2.86	0.15	-19.15	0.00
F9	Frontier Airlines Inc.	685	1.99	0.14	13.73	0.00
YV	Mesa Airlines Inc.	601	0.78	0.16	4.89	0.00
HA	Hawaiian Airlines Inc.	342	1.34	0.27	4.96	0.00
OO	SkyWest Airlines Inc.	32	3.50	0.67	5.26	0.00

lm_rlt3 %>% filter(carrier!='UA') %>%
  ggplot(aes(x = carrier, y = estimate)) + geom_col() +
  labs(title = "Mean Air Time Compared to United Airlines: Robustness Check")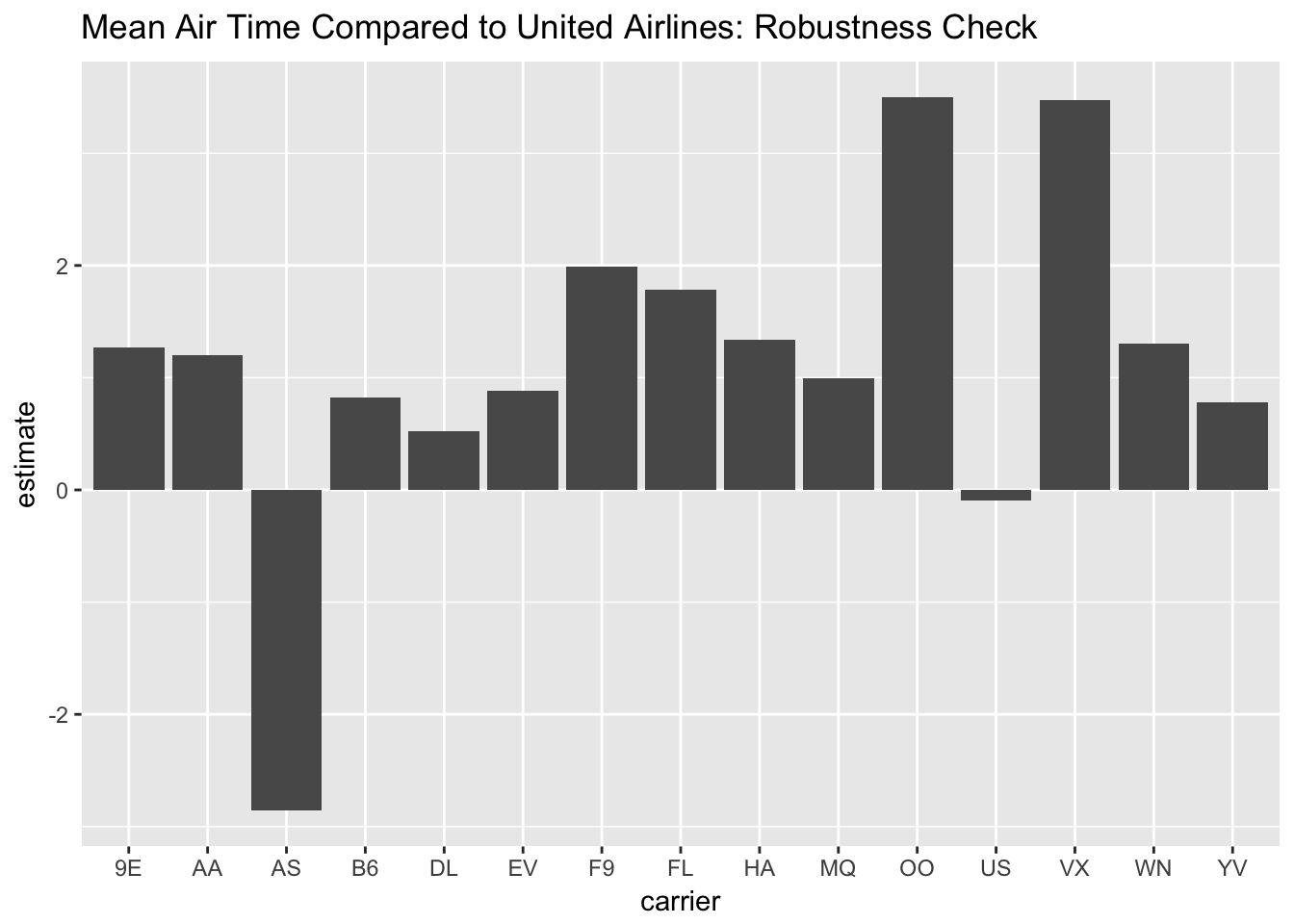

The point estimates should be approximately what we would obtain if we regress air_time on the fixed effects of carrier, dest, and time_hour. However, the standard errors are not correctly displayed in the table because the centered variable has a smaller total variation compared to the original air_time variable. (Correct standard errors can be obtained, for example, through a bootstrapping technique.)

Overall, we see again a tendency that lower-cost carriers like Sky West Airlines, Virgin America, Frontier Airlines, and Air Tran show particularly longer air time than United Airlines. Jet Blue Airways, another low-cost carrier, shows a less obvious difference from United Airlines, possibly suggesting that their operation focused on the East Cost is efficient for the flights departing from New York City. Hawaiian Airlines and Alaskan Airlines appear to be somewhat different from other carriers perhaps because they are more specialized in particular flight destinations compared to their rivals. In particular, the flights to Hawaii may have distinct delay patterns that are concentrated on peak vacation seasons.